最近更新平面设计影视后期全站导航

您的位置: 首页> AI模型

一文读懂 Transformer：从「为什么需要它」到「它为什么能赢」

匿名上传

发布时间:2026-02-02 21:12:01

自 2017 年论文 《Attention Is All You Need》 提出以来，Transformer 成为了 NLP 乃至多模态（CV、语音等）的核心基础架构。

BERT、GPT、T5 看似任务不同，但本质上都是 Transformer 在不同设定下的“结构取舍”：

BERT：Encoder-only，适合双向理解（MLM 预训练）。
GPT：Decoder-only，适合自回归生成（下一词预测）。
T5：Encoder–Decoder，把任务统一成 text-to-text 形式（seq2seq）。

本文将结合结构图 + 模块拆解图，从「为什么需要 Transformer」出发，一步步拆解其设计逻辑、核心模块细节与工程实现直觉，帮你真正吃透 Transformer 的本质。

一、为什么 RNN / CNN 不够用？

1.1 RNN 的核心问题

RNN（循环神经网络）通过“时间步递归”的方式建模序列数据，其核心是将上一时刻的隐藏状态传递到当前时刻，从而捕捉序列依赖。但这种结构天然存在两个结构性缺陷。

（1）强顺序依赖，难以并行计算

在 RNN 的计算逻辑中：

当前时刻 t 的隐藏状态 hₜ，必须依赖上一时刻 t-1 的隐藏状态 hₜ₋₁ 计算完成。
时间维度（序列长度维度）上完全无法并行计算，这是 RNN 最核心的性能瓶颈。

这直接导致两个严重问题：

训练速度慢：序列越长，训练迭代耗时呈线性增长。
GPU 资源利用率低：GPU 擅长并行计算，但 RNN 的时间串行特性使其无法充分利用 GPU 算力。

注意：RNN 并非完全不能并行——在 batch 维度（不同样本之间）和 hidden 维度（隐藏状态的特征维度）仍可并行，但时间维度的串行是不可突破的瓶颈。

RNN 时间展开图：

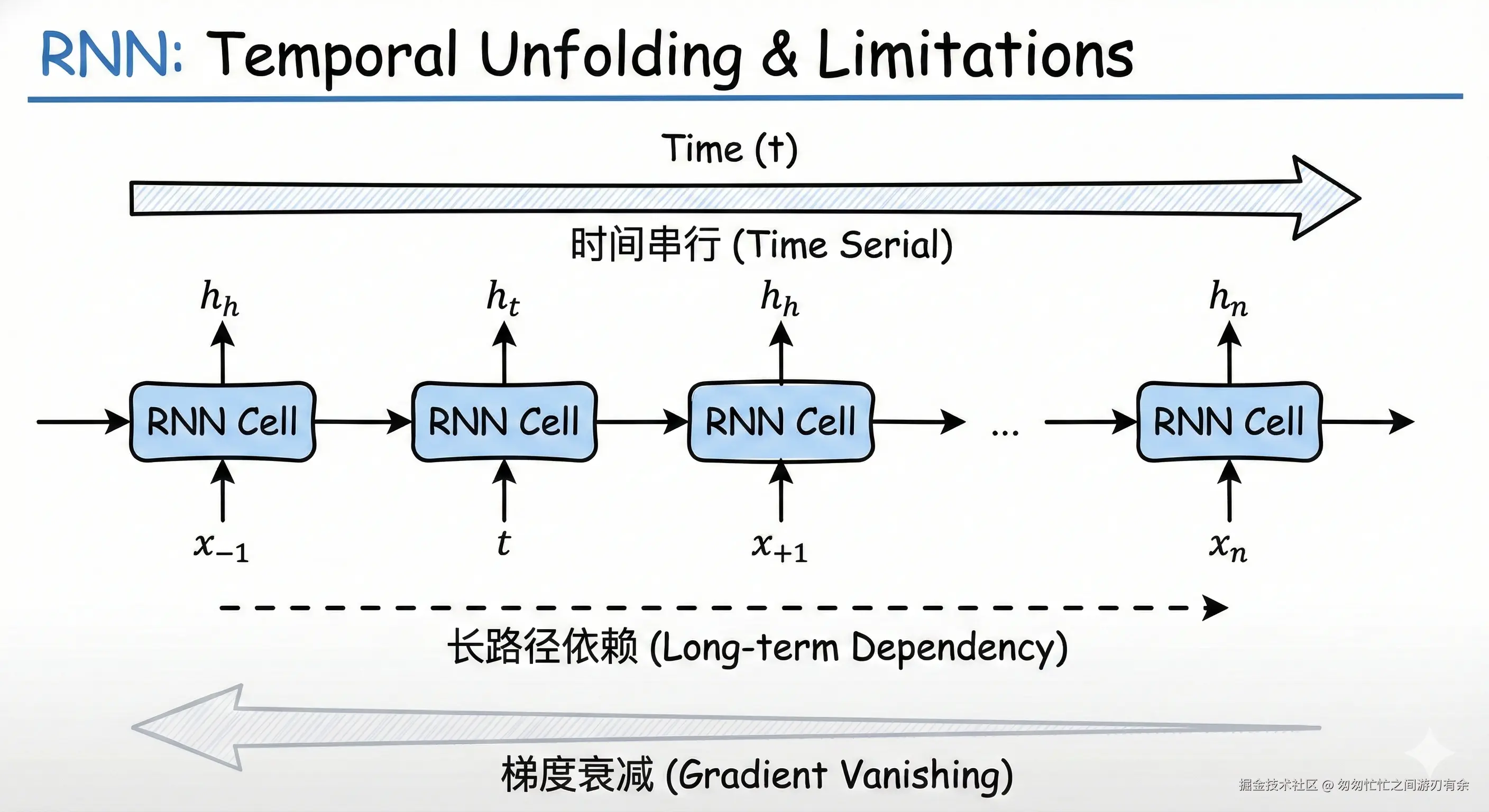
（2）长期依赖建模能力弱

理论上，RNN 可以通过递归传递捕捉任意长度的序列依赖，但在实际训练中：

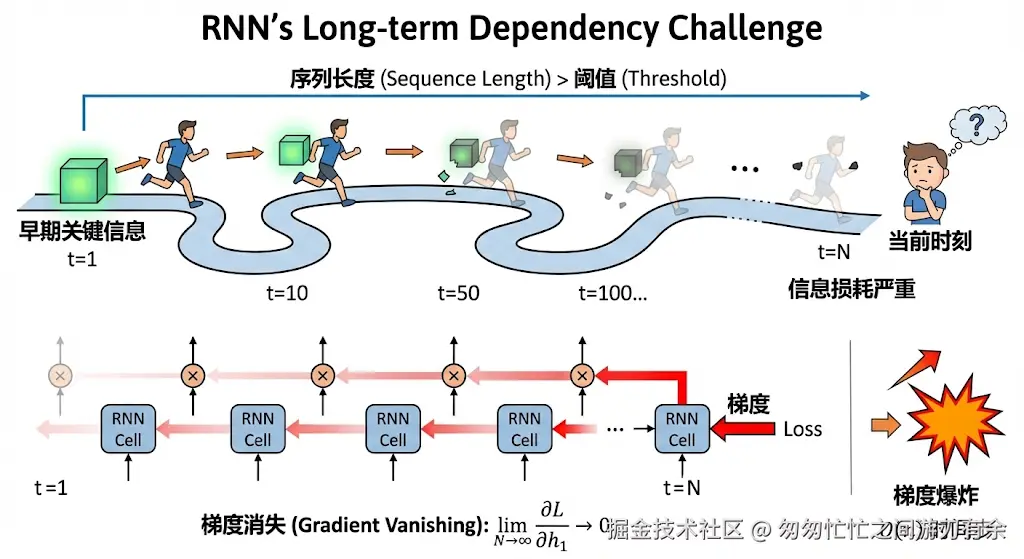
序列长度一旦超过一定阈值（通常几十到上百个 token），就会出现“记不住”早期关键信息的问题。
核心原因是 梯度消失/爆炸：梯度在时间步反向传播时，会经过多次矩阵乘法，导致梯度要么趋近于 0（消失），要么趋近于无穷大（爆炸）。
早期关键信息需要跨越个时间步才能传递到当前时刻，信息损耗严重。

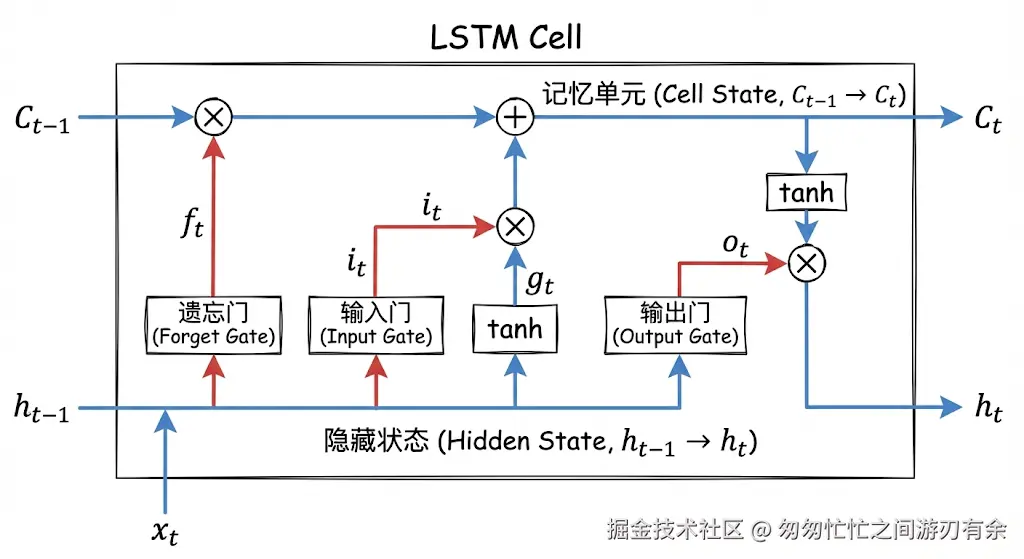
1.2 LSTM 的改进，但没解决根本问题

LSTM（长短期记忆网络）作为 RNN 的变体，通过引入门控机制和记忆单元（Cell State），一定程度上缓解了梯度消失问题：

输入门（Input Gate） ：控制当前时刻的输入信息是否写入记忆单元。
遗忘门（Forget Gate） ：控制上一时刻的记忆单元信息是否保留。
输出门（Output Gate） ：控制记忆单元信息如何映射到当前隐藏状态。
记忆单元（Cell State） ：一条相对独立的信息传递路径，梯度衰减更缓慢

但 LSTM 本质上仍未突破 RNN 的核心局限：

仍然是循环结构，依赖时间步递归传递状态。
仍然是顺序计算，时间维度无法并行的瓶颈未解决。
信息传播路径长度依旧随序列长度线性增长，长期依赖建模能力仍有上限（只是上限比基础 RNN 更高）。

核心结论：LSTM 解决的是“能不能学”（缓解梯度问题），但没解决“算得快不快”（并行性）和“长期依赖能不能精准捕捉”（信息传播路径长）的根本问题。

1.3 CNN：并行了，但视野和依赖建模有限

CNN（卷积神经网络）最初用于图像识别，后来被引入序列建模（如 TextCNN），其核心优势是天然并行性：

通过卷积核滑动提取局部特征，所有卷积操作可并行计算（无顺序依赖）
擅长捕捉序列中的局部模式（如短语、局部语义搭配）

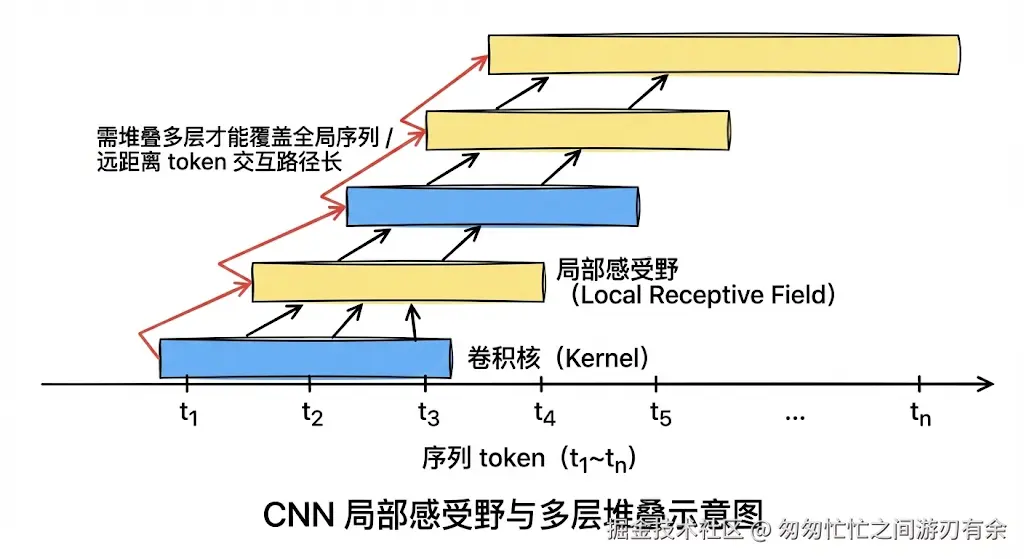
但在序列建模场景中，CNN 存在明显短板：

感受野有限：单个卷积核的感受野是固定的，只能捕捉局部依赖。
长距离依赖建模成本高：要覆盖长序列的全局依赖，需要堆叠大量卷积层，导致网络深度增加、训练难度上升。
交互路径长：两个距离为 k 的 token，需要经过O(log k) 或 O(k) 层卷积才能建立交互，信息传递存在延迟和损耗。

二、Attention Is All You Need：Transfomer的核心突破

Transformer 彻底抛弃了 RNN 的循环结构和 CNN 的卷积结构，其核心思想是： 不再通过时间顺序或局部滑动传递信息，而是让序列中任意位置的 token 直接建立关联，通过注意力机制动态捕捉全局依赖。

Transformer 的设计逻辑是：

不依赖循环结构（无时间步递归）
不通过门控或卷积传递状态
使用注意力机制进行全局信息交互（任意 token 距离为 1）
将序列问题转化为可并行的矩阵计算问题（时间维度完全并行）

Transformer vs RNN 对比图：

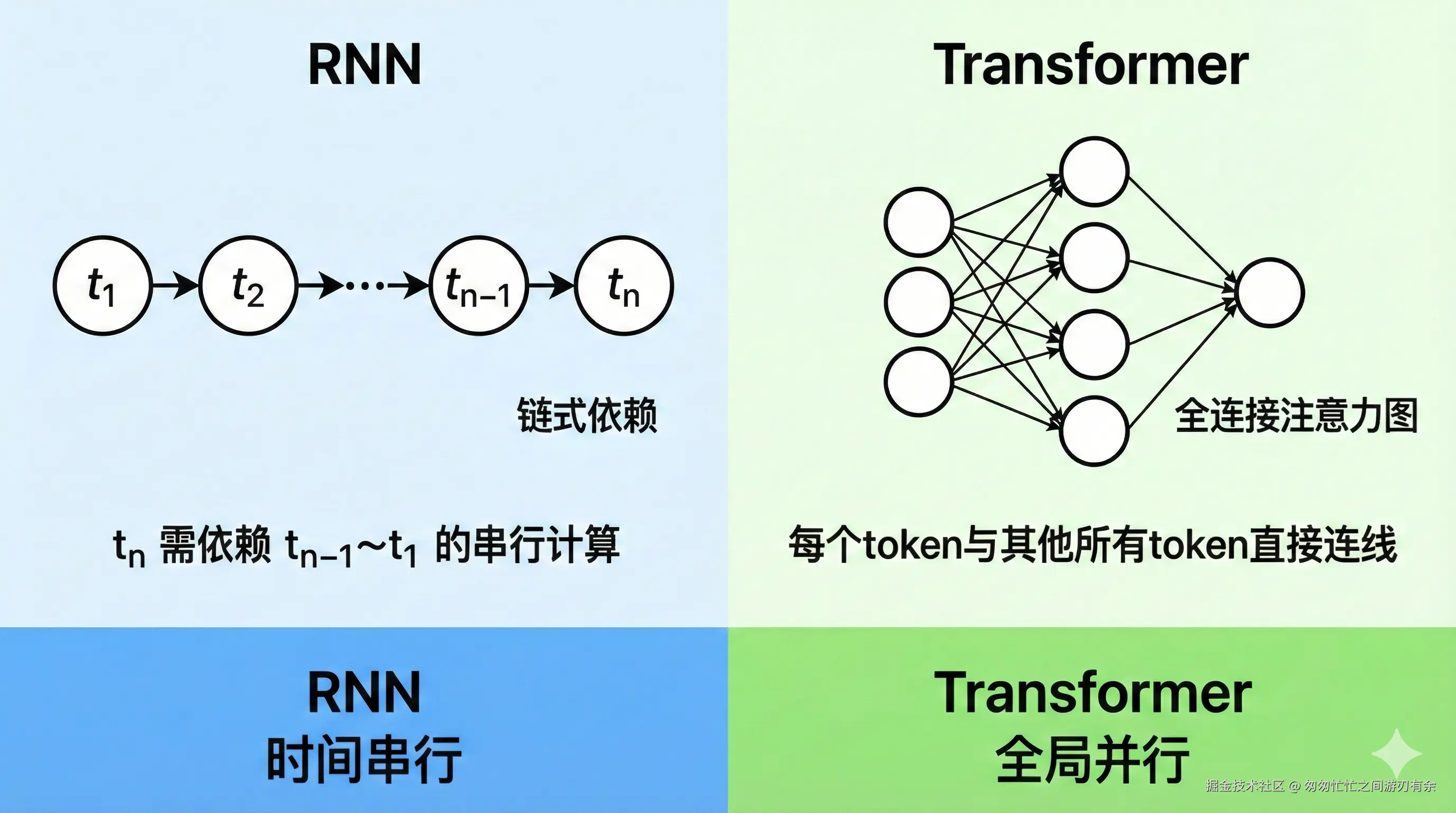
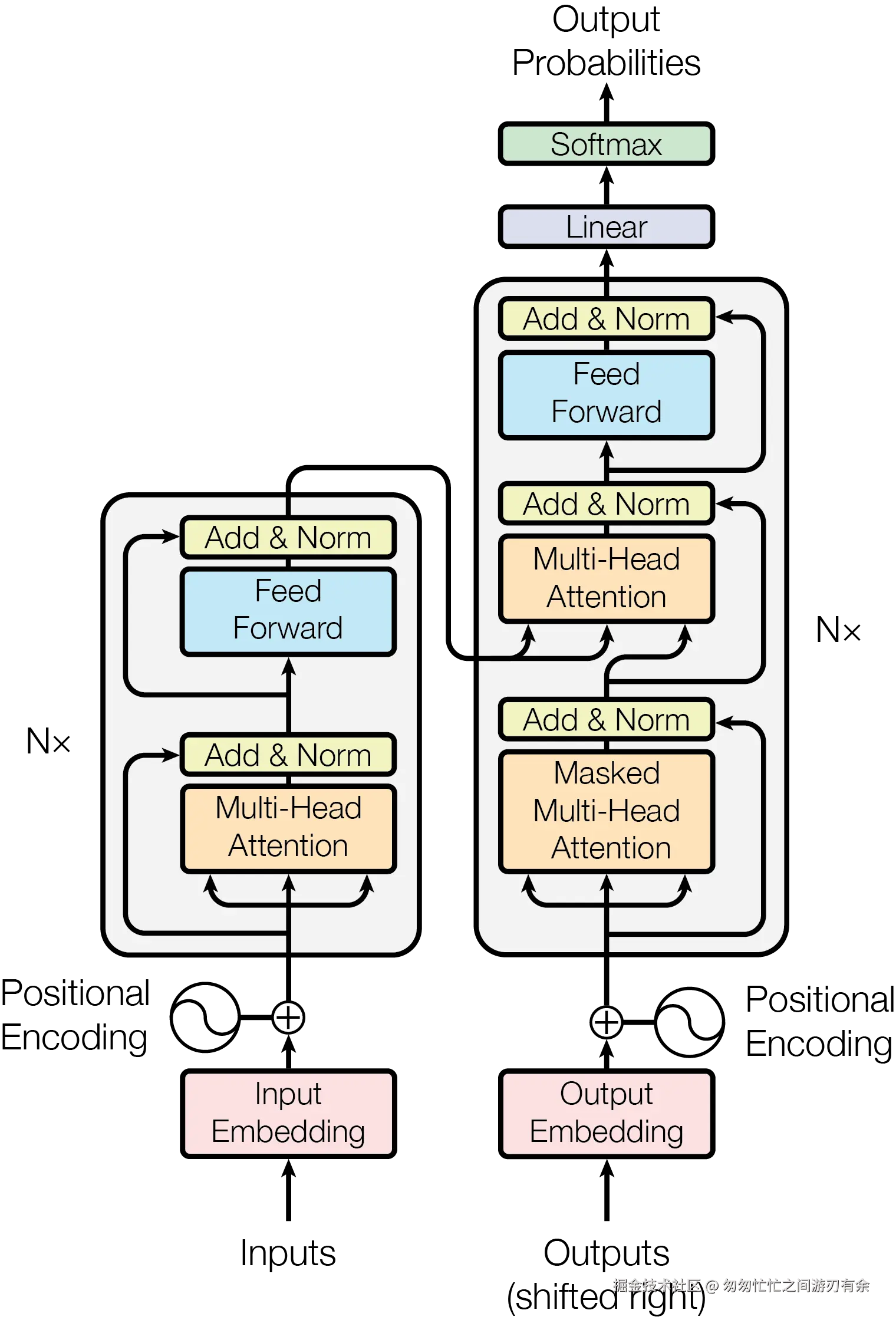
三、Transformer 整体架构（一定要看懂这张图）

Transformer 整体采用“编码器-解码器”（Encoder-Decoder）架构：

Encoder（编码器） ：负责对输入序列进行编码，输出全局上下文表示。
Decoder（解码器） ：负责根据 Encoder 的上下文表示和已生成的序列，自回归地生成目标序列。

在原论文中：

Encoder 堆叠 6 层（每层结构相同，参数独立）。
Decoder 堆叠 6 层（每层结构相同，参数独立）。

关键说明：层数（6 层）是超参数。后续模型如 BERT-base (12层 Encoder)、GPT-3 (96层 Decoder) 均基于此架构调整。

四、Embedding：把词变成可计算的向量

Transformer 处理文本的第一步，是将离散的文本 token（词、子词或字符）映射为连续的向量表示，这一过程为 Embedding（嵌入）：

每个 token 转化为一个固定维度的向量（原论文中维度 d_model = 512 ）。
核心作用：将文本从“离散符号空间”映射到“连续向量空间”，向量距离直接反映语义相似度（如“猫”和“狗”的向量距离比“猫”和“桌子”更近）。

核心认知：Transformer 所有后续计算（注意力、FFN 等），本质上都是在这个高维向量表示空间中，不断重组和更新每个 token 的上下文表示——最终每个 token 的向量都会融合全局上下文信息，成为一个“携带全局语义的向量”。

注意：d_model = 512 并非 Transformer 的本质要求，只是原论文的具体设置。后续模型可根据任务需求调整（如 BERT-base d_model = 768，GPT-2 d_model = 1024），核心是保持嵌入维度与后续模块维度一致。

词 → 向量映射示意图：

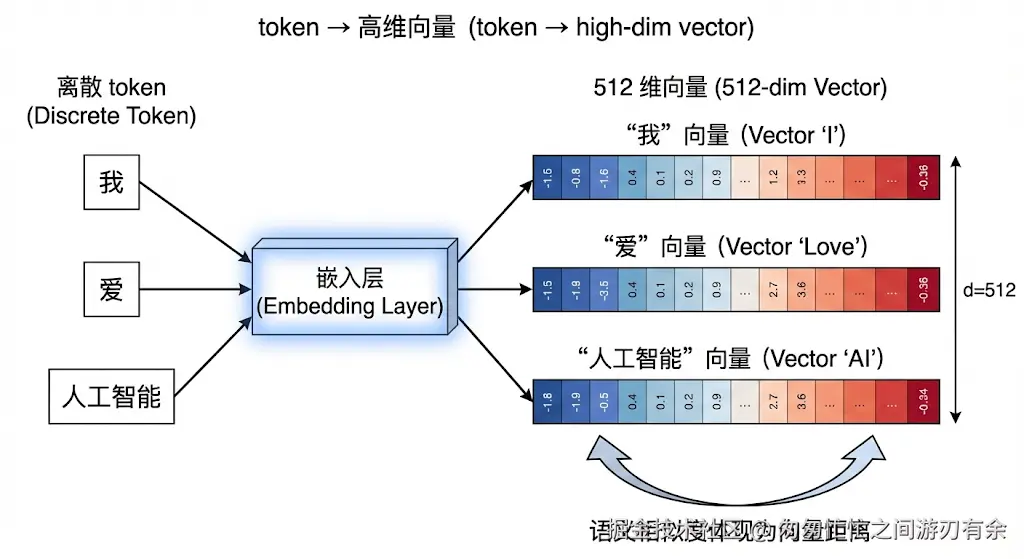
左侧：离散 token（“我”“爱”“人工智能”）
中间：嵌入层（Embedding Layer）
右侧：每个 token 对应的 512 维向量（用矩阵/长条表示）
标注：token → 高维向量，语义相似度体现为向量距离

五、位置编码：没有顺序，模型怎么知道先后？

前文提到，Transformer 抛弃了 RNN 的时间步结构，所有 token 的计算是并行的，模型本身无法区分 token 的顺序（“我吃苹果” vs “苹果吃我”）。因此，必须显式注入位置信息。

5.1 原论文的正弦余弦位置编码

《Attention Is All You Need》采用了固定位置编码。对于位置 $p o s pos$ 和维度索引 $i i$ （ $0 \leq 2 i, 2 i + 1 < d_{m o d e l} 0 le 2i,2i+1 < d_{model}$ ）：

偶数维度： $P E (p o s, 2 i) = \sin (\frac{p o s}{1000 0^{2 i / d_{m o d e l}}}) PE(pos, 2i) = sinleft(frac{pos}{10000^{2i/d_{model}}}right)$
奇数维度： $P E (p o s, 2 i + 1) = \cos (\frac{p o s}{1000 0^{2 i / d_{m o d e l}}}) PE(pos, 2i+1) = cosleft(frac{pos}{10000^{2i/d_{model}}}right)$

最终，输入到 Transformer 第一层的向量是：

I n p u t = T o k e n E m b e d d i n g + P o s i t i o n a l E n c o d i n g Input = TokenEmbedding + PositionalEncoding

（注：两者维度必须一致，均为 d_model，直接逐元素相加）

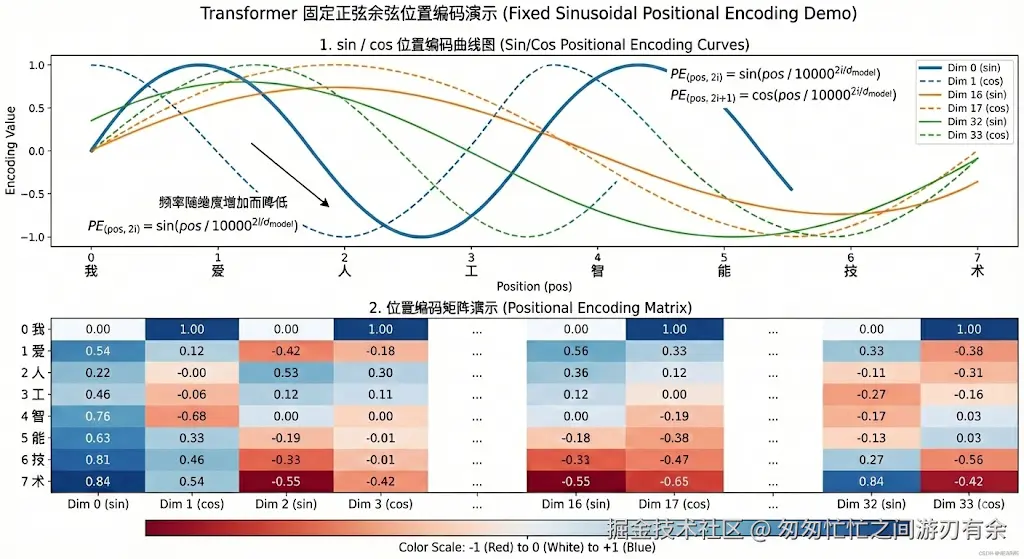
5.2 后续位置编码优化方案（补充）

Transformer 原论文中使用的固定正弦位置编码并非唯一方案。随着模型规模和任务复杂度的提升，后续研究根据不同需求提出了更灵活、效果更优的位置编码或位置信息注入方式：

可学习位置编码（BERT、GPT-2 / GPT-3）
将位置编码设计为可训练参数，与 token embedding 一起端到端学习，能够更好地适配具体任务和数据分布。但由于位置是“绝对建模”的，可学习位置编码在超长序列或长度外推场景下泛化能力有限。

RoPE（旋转位置编码，LLaMA、GPT-NeoX 等）
通过对 Query / Key 向量施加位置相关的旋转变换，将位置信息隐式融入注意力计算过程。RoPE 天然建模相对位置信息，并在长序列外推方面表现稳定，已成为当前大语言模型中最主流的位置编码方案之一。

相对位置偏置（Relative Position Bias，T5）
不直接向 embedding 注入位置信息，而是在注意力分数计算阶段引入 token 间相对位置的偏置项，使模型更高效地捕捉相对依赖关系，尤其适合编码器–解码器结构和文本生成任务。

ALiBi（Attention with Linear Biases）
通过在注意力分数中引入与距离线性相关的衰减偏置来表达位置信息，无需额外的位置编码参数，结构极其简洁，并具备良好的长度泛化能力，已被 BLOOM、MPT 等模型采用，也在更大规模模型中受到关注。

Transformer 位置编码演进对比表：

位置编码方式	代表模型	注入位置	长序列泛化	主要优点	主要局限
固定正弦位置编码	Transformer 原论文	Embedding 层	️ 一般	无参数、理论优雅、可外推	表达能力有限，对复杂语义位置不敏感
可学习绝对位置编码	BERT、GPT-2、GPT-3	Embedding 层	较差	灵活、易训练、适配具体任务	依赖训练长度，超长序列泛化差
相对位置偏置（RPB）	T5	Attention Score	️ 中等	高效建模相对依赖，适合生成任务	设计复杂，依赖 bucket / 超参
RoPE（旋转位置编码）	LLaMA、GPT-NeoX	Q / K 向量	强	结构简洁、长序列稳定、效果好	实现稍复杂，对维度有约束
ALiBi	BLOOM、MPT	Attention Score	强	无位置参数、极简、外推能力好	表达能力相对受限

注：

“注入位置”指位置信息进入模型计算流程的阶段
“长序列泛化”指模型在超过训练长度时的稳定性表现

六、注意力机制：Transformer 的灵魂

注意力机制是 Transformer 实现“全局信息交互”的核心，其本质是：

在计算当前 token 的上下文表示时，序列中其他所有 token 的信息，哪些更重要？应该分配多少权重？

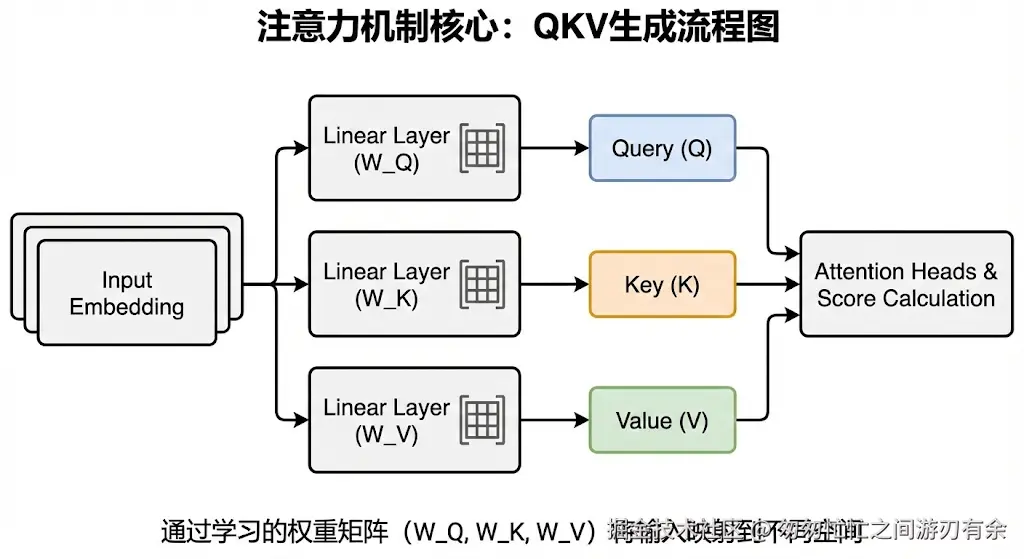
为了实现这一目标，Transformer 引入了 Q（Query，查询）、K（Key，键）、V（Value，值）三个核心向量，这是理解注意力机制的关键。

6.1 Q / K / V 的直觉理解

Query（Q） ：当前 token 的“查询”向量（我要查什么？）（比如“我”这个 token，想知道句子中其他词与“我”的语义关联）。
Key（K） ：被查询 token 的“键”向量（标签是什么？）（比如“爱”这个 token 的 Key 向量，体现其语义特征）。
Value（V） ：被查询 token 的“值”向量（实际包含的内容）（比如“爱”的语义内容）。

核心逻辑：对于当前 token，用 Query 与上下文中所有 Key 计算相关性（匹配程度），通过 softmax 将相关性分数归一化为注意力权重，再用这些权重对对应的 Value 进行加权求和，最终得到一个融合了全局上下文关键信息的表示。

6.2 缩放点击注意力（Scaled Dot-Product Attention）

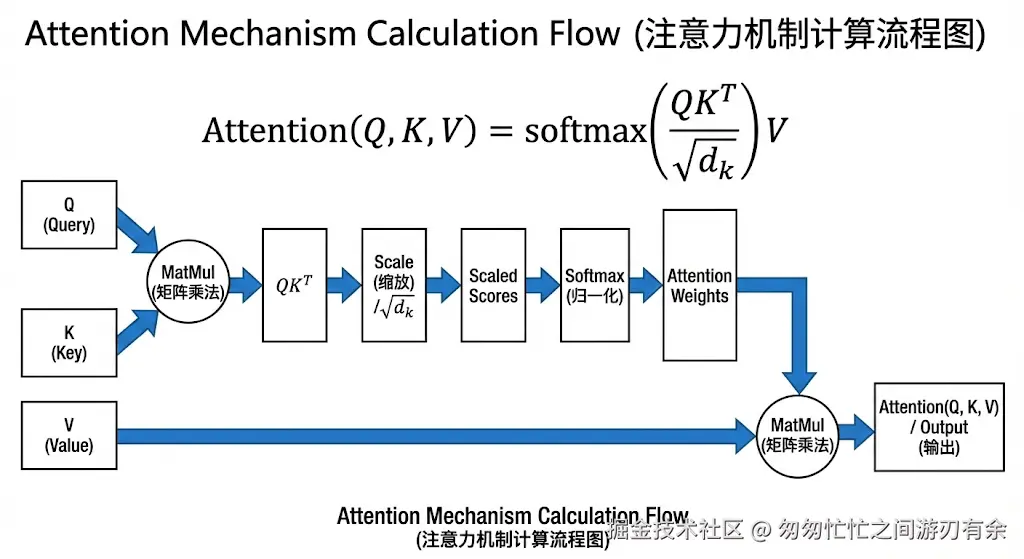
计算过程分为 3 步，核心是“相似度计算→权重归一化→加权求和”：

过程一：计算Query和Key的点积相似度

给定查询矩阵 $Q Q$ 、键矩阵 $K K$ 和值矩阵 $V V$ ，首先通过点积计算 Query 与 Key 之间的相关性：

Q \cdot K^{T} Q cdot K^T

点积结果衡量了每个 Query 与所有 Key 的匹配程度，数值越大表示相关性越强。

过程二：缩放并进行 Softmax 归一化

当维度 $d_{k} d_k$ 较大时，点积结果的数值容易变得过大，从而导致 Softmax 进入饱和区（梯度趋近于 0）、训练不稳定。因此论文中引入了 缩放因子 $\sqrt{d_{k}} sqrt{d_k}$ ：

\frac{Q K^{T}}{\sqrt{d_{k}}} frac{QK^{T}}{sqrt{d_k}}

然后对结果进行 Softmax 操作，得到注意力权重：

softmax (\frac{Q K^{T}}{\sqrt{d_{k}}}) text{softmax}left(frac{QK^{T}}{sqrt{d_k}}right)

Softmax 的作用是：

将相关性分数转换为概率分布
每一行的权重之和为 1

过程三：对 Value 进行加权求和

最后，使用得到的注意力权重对 Value 进行加权求和（权重×V），生成最终的注意力输出（融合了全局上下文信息）：

A t t e n t i o n (Q, K, V) = softmax (\frac{Q K^{T}}{\sqrt{d_{k}}}) V Attention(Q, K, V) = text{softmax}left( frac{QK^T}{sqrt{d_k}} right) V

其中：

每个 Query 会根据其与 Key 的相关性，从 Value 中“聚焦”不同的信息
输出仍然是一个向量序列，用于后续的 Transformer 子层

七、自注意力（Self-Attention）：序列内部的全局交互

在传统的编码器-解码器架构中，注意力往往发生在“源语言”和“目标语言”之间。而自注意力的独特之处在于： $Q u e r y 、 K e y 和 V a l u e Query、Key 和 Value$ 全都来自于同一个输入序列。

7.1 什么是“自”注意力？

简单来说，自注意力让模型在处理序列中的每一个词时，都能“环顾四周”，看看同一个句子里的其他词对理解当前词有什么帮助。

直观例子：

7.2 从输入到 $Q / K / V Q/K/V$ 的演变

在实际的 Transformer 代码实现中， $Q 、 K 、 V Q、K、V$ 并不是凭空产生的，而是通过对输入向量进行线性变换（矩阵乘法）得到的：

输入矩阵 $X X$ ：假设输入是一组词向量组成的矩阵（维度为 $n \times d_{m o d e l} n times d_{model}$ ，其中 $n n$ 是序列长度， $d_{m o d e l} d_{model}$ 是隐藏维度）。
权重矩阵 $W^{Q}, W^{K}, W^{V} W^Q, W^K, W^V$ ：模型拥有三组可学习的参数矩阵。
自注意力层会学习三组投影矩阵，把 $X X$ 映射为 $Q / K / V Q/K/V$ ：

$Q = X \cdot W^{Q} Q = X cdot W^Q$
$K = X \cdot W^{K} K = X cdot W^K$
$V = X \cdot W^{V} V = X cdot W^V$

其中：

$W^{Q}, W^{K} \in R^{d_{m o d e l} \times d_{k}} W^Q, W^K in mathbb{R}^{d_{model} times d_k}$
$W^{V} \in R^{d_{m o d e l} \times d_{v}} W^V in mathbb{R}^{d_{model} times d_v}$

为什么要多此一举进行线性变换？ 如果直接用 $X X$ 代替 $Q 、 K 、 V Q、K、V$ ，模型捕捉特征的能力会非常局限。通过引入 $W^{Q}, W^{K}, W^{V} W^Q, W^K, W^V$ ，模型可以学习如何从不同的维度去提取信息的“身份”（Key）、“需求”（Query）和“本质内容”（Value）。

7.3 自注意力的核心优势

相比于传统的循环神经网络（RNN）或卷积神经网络（CNN），自注意力拥有两个“近乎作弊”的优点：

特性	RNN	CNN	自注意力 (Self-Attention)
长距离依赖	难（梯度消失/爆炸）	有限（受限于卷积核大小）	极强（全局直接连接）
并行计算	差（必须按顺序计算）	优	优（矩阵运算一次完成）
计算复杂度	$O (n \cdot d^{2}) O(n cdot d^2)$	$O (k \cdot n \cdot d^{2}) O(k cdot n cdot d^2)$	$O (n^{2} \cdot d) O(n^2 cdot d)$

注： $n n$ 为序列长度， $d d$ 为向量维度。在 $d d$ 较大而 $n n$ 相对较小时，自注意力的效率惊人。

7.4 一个更“人话”的例子：指代消解

句子：

“他”到底指谁？
传统 RNN/卷积很难一步捕捉这种跨距离依赖，而自注意力会让“他”这个 token 的 Query 去匹配句子里所有 token 的 Key：

它可能会对“小明”的 Key 打更高分
Softmax 后得到更大的权重
最终“他”的输出向量会吸收更多来自“小明”的 Value 信息

于是模型在后续层（或输出层）就更容易判断“他”=“小明”。

自注意力在很多任务里最常见的贡献就是：

建模长距离依赖
捕捉全局语义关系
动态选择上下文信息源

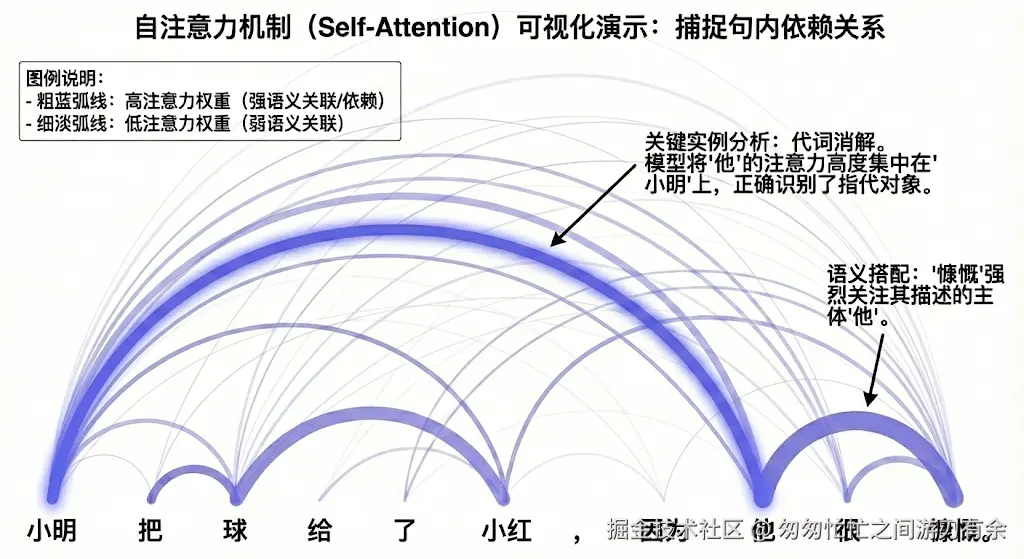
自注意力机制打破了空间的限制，它不再受限于“距离”。无论两个词相隔多远，只要它们在语义上有联系，自注意力就能通过点积运算将它们“连接”在一起。

八、多头自注意力（Multi-Head Self-Attention）：让模型“同时从多个角度看问题”

如果说自注意力（Self-Attention）是让模型学会了“环顾四周”，那么多头注意力（Multi-Head Attention） 则是让模型拥有了“多重人格”，能够同时从多个不同的维度去审视同一个句子。

8.1 为什么需要“多头”

如果只有单头注意力，注意力权重矩阵（ $n \times n n times n$ ）通常会倾向于捕捉某一种主导关系，比如：

语义相似（同义/近义）
句法依赖（主谓宾、修饰关系）
指代关系（他/她/它指谁）
局部短语（相邻词组）

但真实语言里，这些关系往往是同时存在的。
多头的直觉就是：让不同的头分工——每个头学会一种“关注策略”。

你可以把它类比成一个团队开会：

头1：关注语法结构（主谓宾）
头2：关注实体与指代（谁指谁）
头3：关注情感/强弱词
头4：关注长距离依赖

最后把大家的观点汇总，得到更全面的表示。

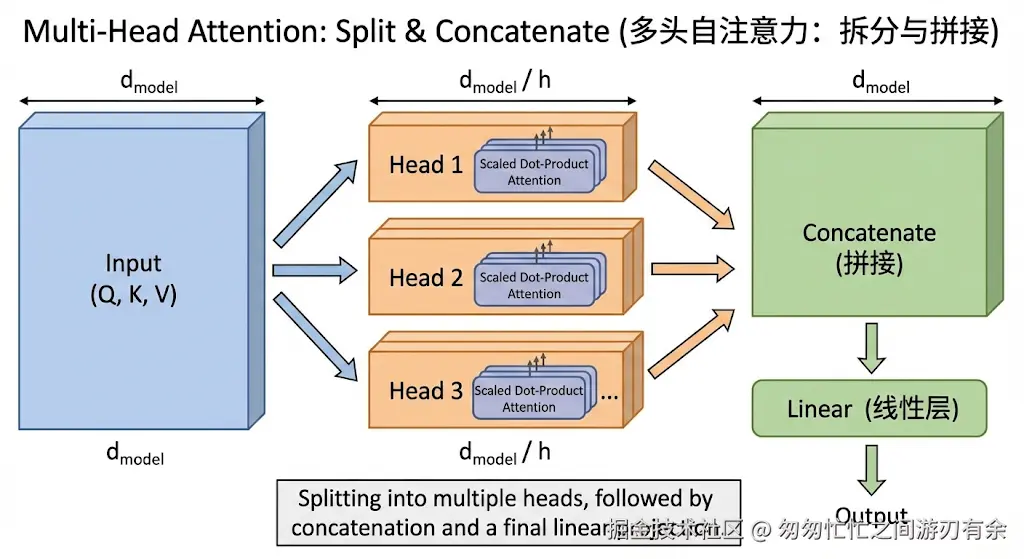
8.2 多头注意力的执行流程

多头注意力的实现并非简单的重复，而是一个“先拆分、再并行、后合并”的过程：

线性变换（Linear） ：将输入的 $Q, K, V Q, K, V$ 分别通过 $h h$ （原论文 $h = 8 h=8$ ）组不同的线性映射，每个头部的维度为 $d_{k} = d_{m o d e l} / h d_k = d_{model} / h$ （原论文 $d_{m o d e l} = 512 ， d_{k} = 64 d_{model}=512，d_k=64$ ），投射到较低维度的子空间中。
并行计算（Scaled Dot-Product Attention） ：每一组映射后的 $Q_{i}, K_{i}, V_{i} Q_i, K_i, V_i$ 独立进行缩放点积注意力计算，得到 $h h$ 个输出结果 $h e a d_{i} head_i$ 。
拼接（Concat） ：将所有头的输出结果按列拼接在一起，恢复到原始的维度。
最终映射（Linear） ：通过一个最终的线性变换矩阵 $W^{O} W^O$ ，将拼接后的多头特征进行融合。

8.3 多头自注意力的核心公式

设输入为：

X \in R^{n \times d_{m o d e l}} X in mathbb{R}^{n times d_{model}}

多头注意力会把注意力计算拆成 $h h$ 个头（head），每个头都有自己的一套投影矩阵：

{head}_{i} = Attention (X W_{i}^{Q}, X W_{i}^{K}, X W_{i}^{V}) text{head}_i = text{Attention}(XW_i^Q, XW_i^K, XW_i^V)

其中：

$W_{i}^{Q} \in R^{d_{m o d e l} \times d_{k}} W_i^Q in mathbb{R}^{d_{model} times d_k}$
$W_{i}^{K} \in R^{d_{m o d e l} \times d_{k}} W_i^K in mathbb{R}^{d_{model} times d_k}$
$W_{i}^{V} \in R^{d_{m o d e l} \times d_{v}} W_i^V in mathbb{R}^{d_{model} times d_v}$

每个 head 会输出：

h e a d_{i} \in R^{d_{m o d e l} \times d_{v}} head_i in mathbb{R}^{d_{model} times d_v}

然后把所有 head 在最后一个维度拼接（concat）：

Concat ({head}_{1}, \dots, {head}_{h}) \in R^{n \times (h \cdot d_{v})} text{Concat}(text{head}_1, dots, text{head}_h) in mathbb{R}^{n times (h cdot d_v)}

最后再通过一个线性层投影回 $d_{m o d e l} d_{model}$ 维：

MultiHead (X) = Concat ({head}_{1}, \dots, {head}_{h}) W^{O} text{MultiHead}(X) = text{Concat}(text{head}_1, dots, text{head}_h)W^O

其中：

W^{O} \in R^{(h \cdot d_{v}) \times d_{m o d e l}} W^O in mathbb{R}^{(h cdot d_v) times d_{model}}

8.4 维度怎么选？为什么常见是 $d_{k} = d_{v} = d_{m o d e l} / h d_k=d_v=d_{model}/h$

实际实现中，通常会让每个头的维度更小，满足：

d_{k} = d_{v} = \frac{d_{m o d e l}}{h} d_k=d_v=frac{d_{model}}h

这样拼接后正好回到原维度：

h \cdot d_{v} = h \cdot \frac{d_{m o d e l}}{h} = d_{m o d e l} h cdot d_v=h cdot frac{d_{model}}h = d_{model}

这背后有一个很现实的考虑：控制计算量。

注意力的核心成本在 $Q K^{T} QK^T$ ：

单头： $Q \in R^{n \times d_{m o d e l}} Q in mathbb{R}^{n times d_{model}}$ ，成本约 $O (n^{2} \cdot d_{m o d e l}) O(n^2 cdot d_{model})$
多头：虽然有 $h h$ 次注意力，但每次用更小的 $d_{k} d_k$ ，总成本仍大致是：

h \cdot O (n^{2} \cdot \frac{d_{m o d e l}}{h}) \approx O (n^{2} \cdot d_{m o d e l}) h cdot O(n^2 cdot frac{d_{model}}{h}) approx O(n^2 cdot d_{model})

也就是说：

多头带来表达能力提升
计算量总体不显著增加（维度按比例切分时）

8.4 多头注意力的“信息融合”到底在融合什么？

把 concat + 线性层 $W^{O} W^O$ 看成一个“汇总器”：

concat：把不同头学到的不同关系特征堆在一起
$W^{O} W^O$ ：再学习如何把这些特征重新混合、压回 $d_{m o d e l} d_{model}$

这一步非常关键，因为它让模型不只是“多看几眼”，而是能学会：

哪些头在当前任务更重要
什么时候该依赖语法头，什么时候该依赖指代头
头与头之间的互补怎么组合

九、残差连接 + 层归一化（Add & Norm）：深层网络的“稳定器”

随着网络加深，训练常见两类问题会被放大：梯度传递困难（梯度衰减或信号被层层变换“冲淡”）与数值/分布不稳定（激活值尺度漂移导致训练抖动）。Transformer 用一套非常经典的组合拳 —— Residual（Add）+ LayerNorm（Norm） —— 来稳住深层堆叠的训练。

9.1 残差连接（Residual Connection）：信息的高速公路

残差连接（Skip Connection）最早在 ResNet 中系统化流行起来。它的核心思想是：让子层学习“增量”而不是“从零重建” ，同时为信息与梯度提供一条绕开复杂变换的直通路径。

逻辑表达：

假设子层（如自注意力层）的操作为 $S u b l a y e r (x) Sublayer(x)$ ，那么残差连接后的输出为：
$O u t p u t = x + S u b l a y e r (x) Output = x + Sublayer(x)$
为什么有效？

1. 更顺畅的梯度通路：

因为
$\frac{\partial y}{\partial x} = I + \frac{\partial Sublayer (x)}{\partial x} frac{partial y}{partial x} = I + frac{partial,text{Sublayer}(x)}{partial x}$
其中 $I I$ 是恒等映射（identity）。这意味着梯度至少可以沿着“恒等分支”回传，不必完全依赖子层的导数项，从而显著缓解深层堆叠的训练困难。

2. 避免表示退化（Degradation）：

如果某个子层学得“不好”甚至接近 0，模型仍可通过残差把输入直接传下去，至少不会比更浅的网络更差；训练会更稳定，也更容易让深层网络真正“用起来”。

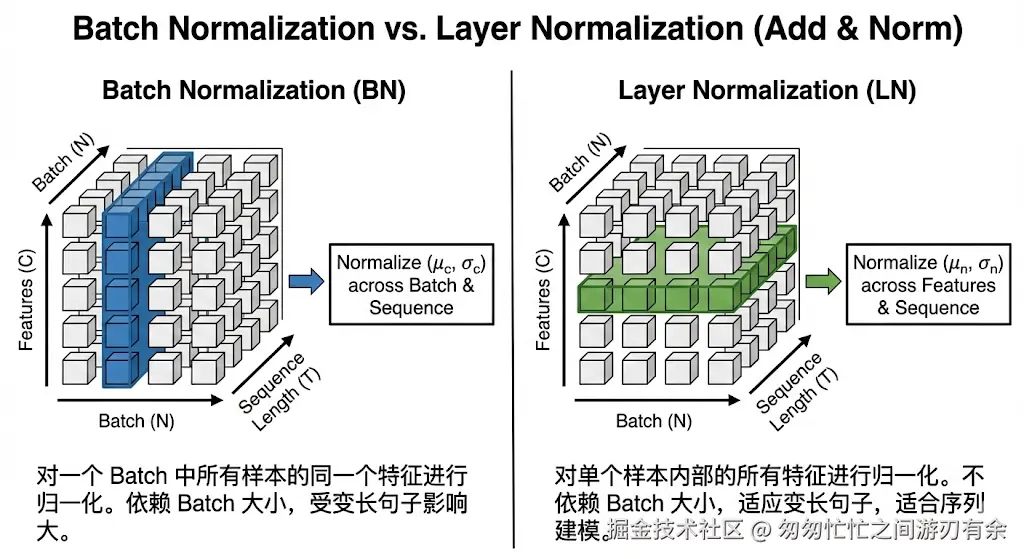
9.2 层归一化（Layer Normalization）：起跑线的统一

残差相加之后，Transformer 通常会接一个 LayerNorm，目的是把激活的尺度拉回到稳定范围，防止深层堆叠时数值分布逐层漂移（过大/过小），从而导致训练发散或震荡。

LayerNorm 做的事情是什么？
对于 Transformer 来说，LayerNorm 通常是对每个 token 的隐藏向量（长度为 dmodeld_{text{model}}dmodel）做归一化：每个位置单独算均值与方差，再标准化。
为什么 LayerNorm 更适合 Transformer，而不是 BatchNorm？
- BatchNorm（批归一化） ：依赖一个 batch 内的统计量（均值/方差）。这会让它对 batch size、数据分布波动、在线推理形态更敏感；在 NLP/序列任务中还要处理 padding/mask，工程上更麻烦，也更不稳定。
- LayerNorm（层归一化） ：对单个样本、单个位置的隐藏维度做归一化：
  - 不依赖 batch 统计；
  - batch 很小也能稳定工作；
  - 推理阶段行为与训练更一致，非常适合序列建模与大模型训练。

9.3 组合拳：Add & Norm 的数学全过程

在 Transformer 的代码实现中，每一个模块的完整公式如下：

LayerOutput = LayerNorm (x + Sublayer (x)) text{LayerOutput} = text{LayerNorm}(x + text{Sublayer}(x))

这个过程可以拆解为三步：

计算残差：将原始输入 $x x$ 与经过子层处理后的向量相加。
计算均值与方差：针对当前层的特征向量计算其均值 $μ mu$ 和方差 $σ^{2} sigma^2$ 。
标准化与缩放：
$\hat{x} = \frac{x - μ}{\sqrt{σ^{2} + ϵ}} \cdot γ + β hat{x} = frac{x - mu}{sqrt{sigma^2 + epsilon}} cdot gamma + beta$
其中 $γ gamma$ 和 $β beta$ 是可学习的参数，让模型有能力还原出最适合的分布。

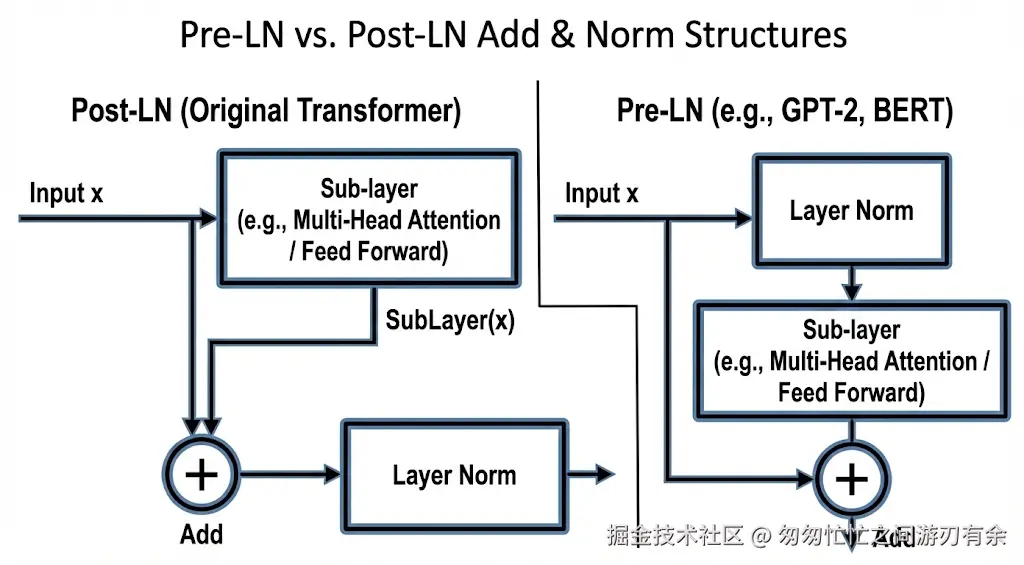
9.4 深度讨论：Post-LN vs Pre-LN

LayerNorm 放在残差相加的前后，会形成两种主流结构：

Post-LN（原始 Transformer 常见）
$LN (x + Sublayer (x)) text{LN}big(x + text{Sublayer}(x)big)$
Pre-LN（现代大模型更常用）
$x + Sublayer (LN (x)) x + text{Sublayer}(text{LN}(x))$
（工程实现里也常见： $x + Dropout (Sublayer (LN (x))) x + text{Dropout}(text{Sublayer}(text{LN}(x)))$

区别：Pre-LN 把归一化放到子层输入端，让子层始终接收到尺度更稳定的输入。

为什么 Pre-LN 更流行？

更容易训练更深的网络：梯度路径更稳定，深层堆叠时不易出现训练崩溃或损失剧烈震荡；
对学习率与 warmup 更不敏感：很多设置下 Pre-LN 更“皮实”，调参压力更小（但 warmup 在大模型训练中依然常见）。

十、前馈网络（FFN）：每个 token 的“独立思考”

在 Transformer 的 Encoder 和 Decoder 中，每一个多头注意力层后面都紧跟着一个前馈网络层。它的核心特点是：逐位置（Position-wise） 。

10.1 什么是“逐位置”前馈？

“逐位置”意味着这个网络是独立地作用于序列中的每一个 token（词向量）上的。

并行处理：对于句子中的每一个词，FFN 使用的权重矩阵都是完全相同的。
无交互：在这一层，词与词之间没有任何信息交换。它们就像是坐在考场里的学生，各自独立地处理自己手里的卷子。

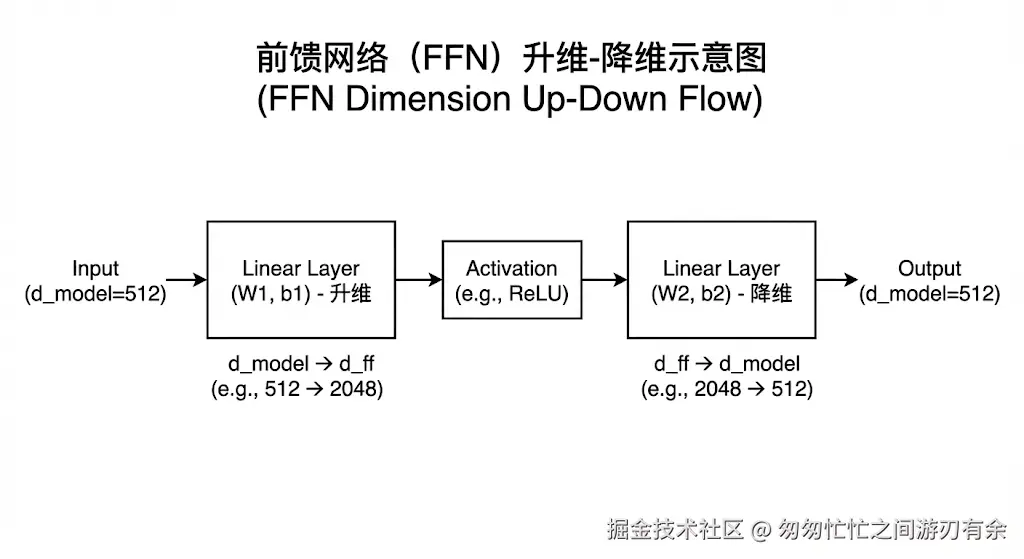
10.2 FFN 的内部构造：升维与降维

FFN 的结构其实非常经典，它由两个全连接层（线性变换）组成，中间夹着一个非线性激活函数。其数学表达式为：

F F N (x) = \max (0, x W_{1} + b_{1}) W_{2} + b_{2} FFN(x) = max(0, xW_1 + b_1)W_2 + b_2

具体的执行步骤如下：

第一层线性变换（升维） ：将输入向量从 $d_{m o d e l} d_{model}$ （通常是 512）映射到一个更高的维度 $d_{f f} d_{ff}$ （通常是 2048）。
非线性激活：使用 ReLU（在原始论文中）或 GeLU（在 GPT 等后续模型中）进行激活。这一步引入了非线性，是模型能够学习复杂模式的关键。
第二层线性变换（降维） ：将 2048 维的空间重新映射回 $d_{m o d e l} d_{model}$ （512 维），以便后续层继续处理。

为什么要先升维再降维？

这种“扩张-收缩”的结构能提供更强的特征提取能力。在 2048 维的高维空间里，模型可以更精细地拆解和重新组合语义特征，就像把一团揉皱的纸展开（升维），看清楚上面的字，再重新折好（降维）传递下去。

10.3 为什么 FFN 必不可少？

你可能会问：既然注意力机制已经能捕捉全局信息了，为什么还要 FFN？

特征转换：注意力机制本质上是做“加权平均”。如果没有 FFN 的非线性变换，无论叠加多少层注意力，最终都只是输入的线性组合。FFN 赋予了模型非线性拟合的能力。
知识存储：许多研究表明，Transformer 学习到的“世界知识”和“模式记忆”大部分都存储在 FFN 的权重矩阵中，而注意力机制更多地起到了导航和路由的作用。

10.4 总结：FFN 的角色

维度	特点
计算对象	独立处理每个 token 的向量
结构	线性层 -> 激活函数 -> 线性层
核心作用	引入非线性、特征转换、存储知识

十一、Encoder vs Decoder：核心差异与场景

如果把 Transformer 比作翻译官，Encoder 就是“深度阅读者” ，负责把原文读透；Decoder 就是“金牌创作者” ，负责把理解的内容转化为流畅的新文本。

11.1 结构上的“三处不同”

虽然它们看起来很像，但 Decoder 相比 Encoder 多了两个关键特征，以及一个特殊的“遮盖”机制。

特性	Encoder (编码器)	Decoder (解码器)
注意力机制	双向（Bidirectional）	单向/掩码（Masked Self-Attention）
层数结构	多头注意力 + FFN	多了一个 Cross-Attention 层
输入方式	一次性输入整个序列	逐个 Token 生成（Auto-regressive）
目标	提取高维语义特征	预测序列中的下一个词

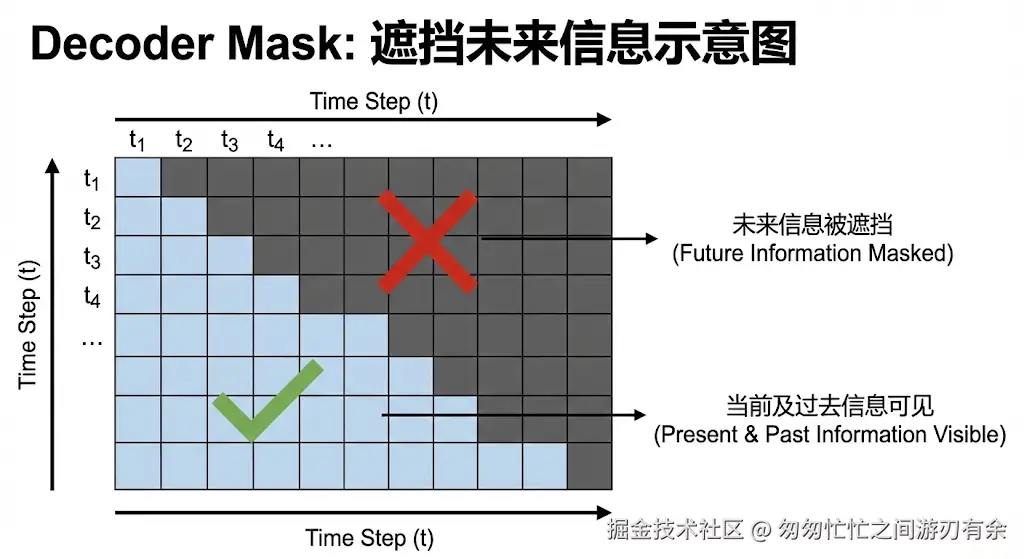
11.2 Decoder 的核心秘密：掩码自注意力（Masked Self-Attention）

这是两者之间最本质的区别。

Encoder 的自由：在计算“我”的语义时，它可以看句子后面的“爱”和“你”。这种“上帝视角”有助于理解全局。
Decoder 的禁忌：在生成翻译时，模型必须模拟真实情况。如果它在预测第二个字时，已经“偷看”了第三个字，那么训练就失去了意义（即“标签泄露”）。

解决办法：Mask（掩码） 在 Decoder 的第一层注意力中，我们会加入一个三角矩阵掩码，强行将当前位置之后的注意力得分设为 $- \infty -infty$ 。这样，模型在计算第 $t t$ 个位置时，只能看到 $t t$ 之前的词。

11.3 桥梁：交叉注意力（Cross-Attention / Encoder-Decoder Attention）

这是 Decoder 特有的第二个子层，也是它与 Encoder 发生互动的时刻：

Query (Q) ：来自 Decoder 前一层的输出（我想写什么？）。
Key (K) & Value (V) ：来自 Encoder 最后一层的输出（原文说了什么？）。

通过这一层，Decoder 在生成每一个字时，都会去 Encoder 的“知识库”里检索相关的信息。

11.4 场景之争：谁才是王者？

随着大模型的发展，Encoder 和 Decoder 各自衍生出了不同的流派：

1. 只用 Encoder（Only Encoder）

代表模型：BERT、RoBERTa。
擅长场景：自然语言理解（NLU） 。如文本分类、情感分析、命名实体识别。它擅长给句子“打分”或“贴标签”，因为它能看到上下文。

2. 只用 Decoder（Only Decoder）

代表模型：GPT 系列、Llama、Mistral。
擅长场景：自然语言生成（NLG） 。这是目前大模型的主流。由于它天生就是为了预测下一个词而设计的，因此在对话、创作、写代码方面表现极强。

3. 完整架构（Encoder-Decoder）

代表模型：T5、BART。
擅长场景：强序列转换。如机器翻译（中翻英）、文本摘要（长变短）。它依然保留了最原始的“理解+生成”逻辑。

总结

Encoder 是“理解专家”，它通过双向注意力榨取信息的精华。
Decoder 是“预测天才”，它通过掩码机制和交叉注意力，在约束中创造序列。

两者相辅相成，构成了 Transformer 架构的阴阳两面。

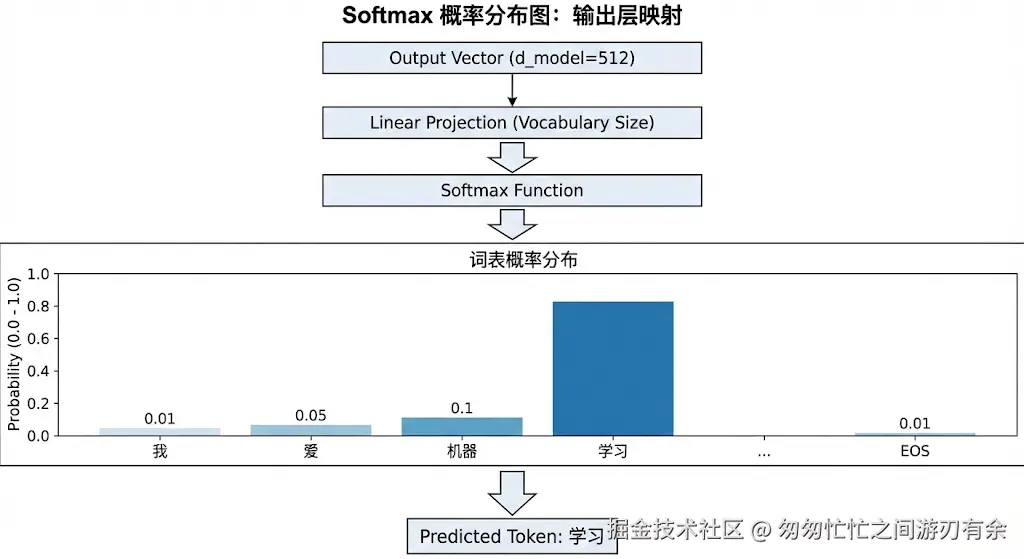
十二、输出层：从向量到词表映射

输出层的任务非常明确：将 Decoder 输出的特征向量映射到词表空间，并计算出下一个词出现的概率。

这一层通常由两个简单的步骤组成：线性变换（Linear） 和 Softmax 归一化。

12.1 线性投影（Linear Projection）

Decoder 最后一层的输出是一个形状为 $[B a t c h, S e q u e n c e, d_{m o d e l}] [Batch, Sequence, d_{model}]$ 的张量。

映射操作：线性层（一个全连接层）会将维度从 $d_{m o d e l} d_{model}$ （如 512）投影到一个巨大的维度——词表大小（Vocabulary Size） （通常在 30,000 到 100,000 之间）。
逻辑得分（Logits） ：投影后的结果被称为 Logits。序列中每个位置都会得到一个长度为“词表大小”的向量，向量中的每个数值代表了对应词表单词的“原始得分”。

12.2 Softmax 归一化：概率化

Logits 的数值范围很大，且难以直观理解。为了进行选择或训练，我们需要通过 Softmax 函数将其转化为概率分布：

$P (y_{i} ∣ y_{< i}, X) = softmax ({Logit}_{i}) P(y_i | y_{<i}, X) = text{softmax}(text{Logit}_i)$

结果：词表中每个单词都会获得一个 $00$ 到 $11$ 之间的概率值。
特性：所有单词的概率之和严格等于 $11$ 。概率最高的单词，就是模型认为“最该出现”的下一个词。

12.3 训练与推理的差异

输出层在模型生命周期的不同阶段，扮演着略有不同的角色：

在训练阶段：计算损失（Loss Calculation）

我们已知“标准答案”（Label）。
将 Softmax 产生的概率分布与真实单词的 One-hot 编码进行对比。
使用 交叉熵损失函数（Cross-Entropy Loss） 来衡量差距，并通过反向传播更新整个模型的参数。

在推理（预测）阶段：解码策略

模型给出了概率分布，但我们如何最终选定那个词？这就涉及到了解码策略：

贪心搜索（Greedy Search） ：每次都选概率最大的那个词。简单高效，但容易陷入局部最优。
束搜索（Beam Search） ：同时保留概率最大的前 $N N$ 个路径，寻找全局最优。
采样（Sampling） ：根据概率分布随机抽一个。这让 AI 回答更具多样性和“创造力”（如 GPT 的 Top-p, Top-k 采样）。

12.4 权重共享（Weight Tying）的小技巧

在很多 Transformer 实现（如原始论文和 BERT/GPT）中，有一个非常聪明的优化：输出层的线性变换矩阵与输入层的 Embedding 矩阵是共享权重的。

逻辑：既然 Embedding 是把词变成向量，线性层是把向量变成词，那么这两个过程在语义空间上应该是互逆的。
好处：极大地减少了模型的参数量（毕竟词表很大），并能提高模型的泛化能力。

十三、为什么 Transformer 能赢？

Transformer 自 2017 年提出后，迅速取代 RNN、CNN 成为 NLP 领域的主流架构，甚至延伸到 CV、语音、多模态等方向——其成功并非偶然，而是源于它在模型表达能力、训练效率和工程可扩展性上的全面胜出。

从本质上看，Transformer 并不是“某一个技巧的改进”，而是一整套重新思考序列建模方式的结果。

具体核心优势拆解：

全局建模能力强：天然捕捉长距离依赖，自注意力机制让任意两个 token 之间的距离都变成 1 次计算，彻底解决了 RNN 长距离依赖衰减的问题。
完全并行计算：训练效率质的飞跃，不再依赖时间步递归，Transformer 可以在 GPU / TPU 上对整个序列并行计算，大幅缩短训练时间。
表达能力更灵活：注意力 ≠ 固定结构，Attention 是数据驱动的动态权重分配，相比 CNN 的固定感受野、RNN 的单向传递，建模方式更自由。
多头机制增强表示多样性，Multi-Head Attention 让模型可以同时关注不同子空间、不同关系模式，提升了表示的丰富度与鲁棒性。
深层网络依然稳定、易训练，残差连接 + 层归一化，使 Transformer 可以堆叠得更深，而不会轻易出现梯度消失或训练崩溃。
架构通用性强，易于迁移与扩展，同一套 Transformer 框架，可以轻松适配 NLP、CV、语音、多模态，并成为大模型时代的统一底座。

一句话总结：

总结

Transformer 之所以能够成为深度学习时代最重要的基础架构之一，并不是偶然的“效果领先”，而是因为它在三个关键维度上同时成立：
理论直觉正确、结构设计简洁、工程实现高效。

1. 理论直觉：模拟人类注意力的本质 (Theoretical Intuition)

Transformer 第一次在数学上完美复刻了人类的“认知直觉”。

从“死记硬背”到“定向搜索” ：传统的 RNN 靠记忆传递信息，容易“忘词”；Transformer 通过 $Q / K / V Q/K/V$ 将语义比作搜索引擎，实现了按需检索，让模型具备了真正的理解力。
空间屏障的消失：在模型眼中，文本不再是一个有先后距离的序列，而是一个全连接的图。无论两个词相隔多远，其交互成本（路径长度）始终是 $O (1) O(1)$ ，彻底解决了长距离依赖问题。

理解 Transformer，就是理解现代深度学习的新范式。

2. 结构设计：极度模块化的对称美学 (Structural Design)

Transformer 的结构设计是“Unix 哲学”在深度学习中的体现：简洁、通用、可组合。

标准化的“积木” ：整个架构由重复的 Block（注意力 + 前馈网络）组成。这种高度标准化的设计，使得模型可以像搭积木一样无限堆叠，从而实现从百万到万亿参数的平滑跨越。
Add & Norm 的平衡艺术：残差连接负责“传得深”，层归一化负责“传得稳”。这两者的引入，解决了深层网络难以训练的顽疾，为深达百层的架构提供了物理保障。

3. 工程实现：GPU 时代的算力收割机 (Engineering Efficiency)

Transformer 真正赢在它对现代算力极其友好，简直是为 GPU 量身定做的。

从“串行”到“矩阵运算” ：它摒弃了 RNN 必须等待上一步计算结果的弊端，将所有计算转化为大规模的矩阵乘法。这完美契合了 GPU 成千上万个核心的并行处理能力。
计算效率的飞跃：在训练阶段，Transformer 的并行度远超传统模型。同样的算力和时间，Transformer 能“喂”进去的数据量是 RNN 的数十倍甚至上百倍，这种规模效应最终导致了智能的“涌现”。

结语：大道至简

Transformer 的伟大在于它用最简单的数学（点积）和最简洁的结构（堆叠），处理了最复杂的问题（自然语言） 。它不仅是目前 NLP 的终点，更是通往通用人工智能（AGI）的起点。

本站提供的所有下载资源均来自互联网，仅提供学习交流使用，版权归原作者所有。如需商业使用，请联系原作者获得授权。如您发现有涉嫌侵权的内容，请联系我们邮箱:alixiixcom@163.com

热门小说大全app

热门小说大全

立即下载